古代は丸い平面(平らな円盤)だと考えられていた地球。実際にはどのような形で、どれくらいの大きさでしょうか。この記事では、地球の概観(地球の形や大きさなど)を解説します。
地球の表面
水の惑星ともいわれる地球。事実、地球には水が豊富にあります。
地球表面について、海岸線を境に陸と海を分けると、陸は地表の約30%を占め、海は地表の約70%を占めます。
陸地の最も高いところは、エベレストで標高8848m。
海底の最も深いところは、マリアナ海溝のチャレンジャー海淵で水深約10920m。
地球表面の高度分布を見ると、陸地は高さ0〜1km、海底は深さ4〜5kmの占める割合が大きいです。
海岸から水深200mぐらいまでの傾斜のきわめて緩い海底を大陸棚といい、地質学的には大陸地域に含まれます。氷期ではなく比較的温暖な間氷期である現在の地球は海面水位が比較的高いため、地質学的には大陸地域である「大陸棚」が水深0〜200mの海底になっています。
大陸棚は全海洋の面積の約17%を占めます。大陸棚の地層中には石油、石炭、天然ガスなどが理蔵されているところもあります。漁場も多く、重要な資源が存在します。
地球の形
古代、地球の形は丸い平面(平らな円盤)だと考えられていました。
しかし、紀元前330年頃、アリストテレス(ギリシャ)は、以下の理由から「地球は球形」と考えました。
- 月食の時(地球が太陽と月の間に入った時)、月に映った地球の影が円形であること
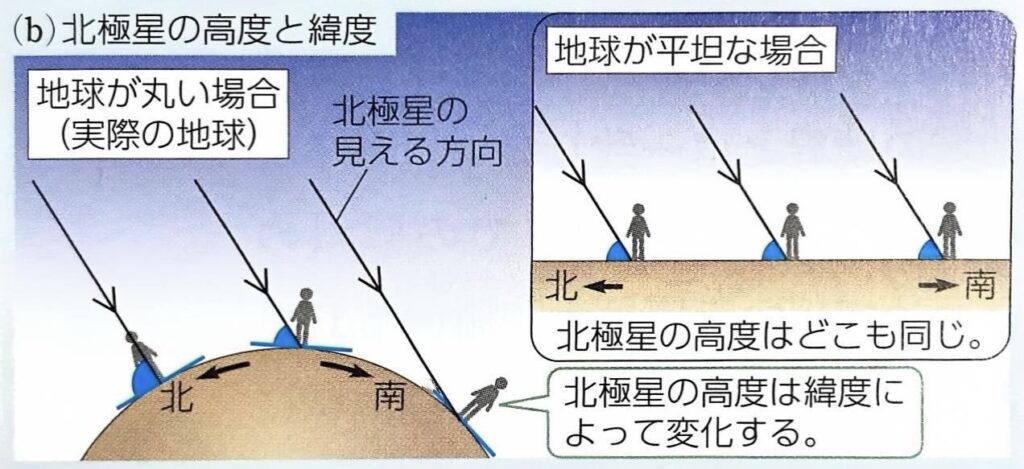
- 地球上を南北に移動すると北極星の高度(見える位置)が変化すること(もし地球が平らであれば、北極星の高度はどこでも同じはず)
さらに、
- 船が陸地に向かう際、最初は山の山頂から見えて、陸地に近づくにつれて徐々に低いところまで見えてくる(もし地球が平らであれば、最初から山頂から低いところまで見えるはず)

ことなども、地球が球形である証拠とされています。
では、地球はボールのような完全な球形なのでしょうか? それは、17世紀に議論がありました。
ホイヘンス(オランダ)は、粘土で作った球体(粘土球)の中心に棒を通して速く回転させると、粘土球の形が横長に扁平になることから、地球も同様に楕円体であると考えました。横長に扁平になるのは、中心の軸(回転軸)から外向きに働く遠心力のためです。
また、ニュートン(イギリス)は、回転による球の変形を理論的に求め、地球は赤道方向にふくらんだ形になることを示しました。
このようなことから、地球の形は、ボールのような完全な球形ではなく、上下から少し押しつぶされたみかんのような、赤道方向にふくらんだ回転楕円体(楕円がその軸のまわりに回転して生じる立体)に近いことが分かりました。
地球の大きさと形に最も近い回転楕円体のことを、特に地球楕円体といいます。
楕円や回転楕円体のつぶれ具合は扁平率で表されます。
\( 扁平率 = \dfrac{赤道半径−極半径}{赤道半径} \)
※赤道半径は、地球の中心から赤道までの距離
※極半径は、地球の中心から極(北極または南極)までの距離
赤道半径≧極半径とすると、扁平率は0〜1の値になります。
扁平率=0だと赤道半径=極半径となり完全な球形です。
扁平率≒1だと極半径≒0となり、平べったい楕円形になります。
後で出てきますが、実際の地球は赤道半径が約6378km、極半径が約6356kmのため、扁平率は0に近く、地球はかなり球形に近い回転楕円体であるということが分かります。
\( 地球の扁平率 ≒ \dfrac{1}{300}\)
地球の大きさ
地球の大きさはどれくらいでしょうか。そして、どのように計算したのでしょうか。
紀元前230年頃、エラストテネス(ギリシャ)は太陽の南中高度を利用して地球の大きさを計算しました。地球が球形であると仮定し、弧の長さ(2地点間の距離)と円の中心角が比例するという関係を使って地球の周囲の長さを求めたのです。
具体的には、約900km離れた2地点(夏至の日の正午に太陽が真上(南中高度が90度)になる地点と、その場所からほぼ真北に約900km離れた地点)で、南中高度差=緯度差=地球断面円の中心角=7.2°であったことから、地球の周囲の長さをAkmとすると、
\( 900 km : 7.2 ° = A km : 360 ° \)
\( A km × 7.2 ° = 900 km × 360 ° \)
\( A km = 900 km × \dfrac{360 °}{7.2 °} = 45000 km \)
※当時はkmという概念がなかったのですが、現代の単位に換算すると約45000kmということです。
現代の科学技術で計測すると、地球の周囲の長さは約40000kmです。
もう少し正確にいうと、赤道1周の距離は約40075km、北極と南極を通る1周(子午線)の距離は約40008kmです。
ここで、「 円周 = 2 × π × 半径 」という関係から、地球の周囲を円と近似すると、
\( 地球半径 = \dfrac{地球の円周約4万km}{2×π} = 約6400km \)
(直径はその倍で約12800km)
※実際の地球は球体ではなく、みかんのように上下から少し押しつぶされた回転楕円体のため、赤道半径が6378.137km、極半径が6356.752kmです。
約6400kmとは、東京からハワイ(ホノルル)、大阪からインド(ムンバイ)くらいの距離です。
地表面のある場所から、地面を真下に約6400km掘っていくと地球の中心にあたり、さらに約6400km進むと地球の裏側の地表面に出てくることになります。
日常生活では、地表は海や山など凹凸の大きい複雑な地形のように感じます。
エベレスト(標高8848m)からチャレンジャー海淵(水深10920m)まで約20kmですが、地球半径約6400kmと比較すると、地球半径の0.3%程度です。人間は地表というごく限られた範囲で生活していることになります。逆にいえば、それくらい地球は大きいということです。
大きさのイメージとして、地球、テニスボール、アルミニウム原子の大きさ(直径)を考えてみます。
アルミニウム原子を約2億倍するとテニスボールの大きさ、テニスボールを約2億倍すると地球の大きさになります。
※素粒子は原子よりもっともっと小さく、宇宙は地球よりもっともっと大きいです。
まとめ
地球の表面について、陸が約30%、海が約70%を占める。陸域の最も高いところはエベレストで標高8848m、海底の最も深いところはマリアナ海溝のチャレンジャー海淵で水深10920m。海岸から水深200mぐらいまでの傾斜のきわめて緩い海底を「大陸棚」という。
地球の形について、紀元前330年頃にアリストテレスは「地球は球形」だと考えた。17世紀にホイヘンスやニュートンは「地球は完全な球形ではなく、赤道方向にふくらんだ回転楕円体」だと考えた。赤道方向にふくらむのは、自転による遠心力が外向きに働くため。
地球の大きさについて、紀元前230年頃にエラストテネスは太陽の南中高度を利用して、地球の周囲の長さを約45000kmだと計算した。現代では約40000km(地球半径は約6400km)とされている。
個人的な感想
・人類の先輩方の洞察力や思考力に脱帽
現代だと学校教育で学び、広く一般に知られている地球の形や大きさ。2000年以上も前に正解にだいぶ近いところまで解明されていて、昔の人の洞察力や思考力に感心しました。
・様々な大きさの物質、その多様性に感激
日常生活では丸さを感じないほどあまりにも大きな地球。一方で原子のようなあまりにも小さな物質もあり、この地球上には様々な大きさの物質が存在しています。その多様性に感激しました。


コメント